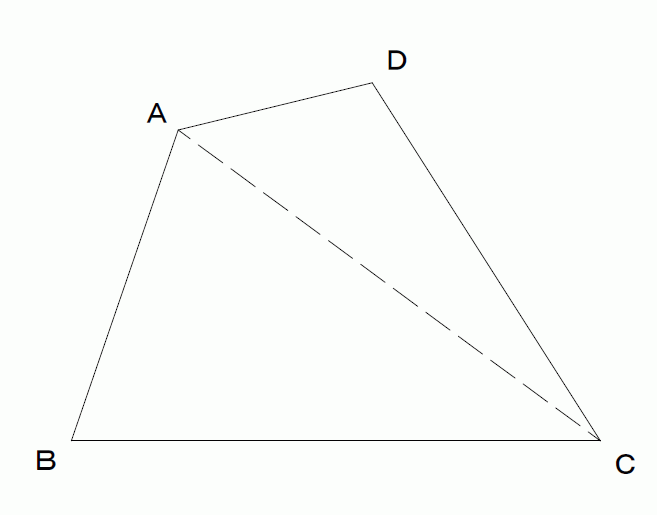
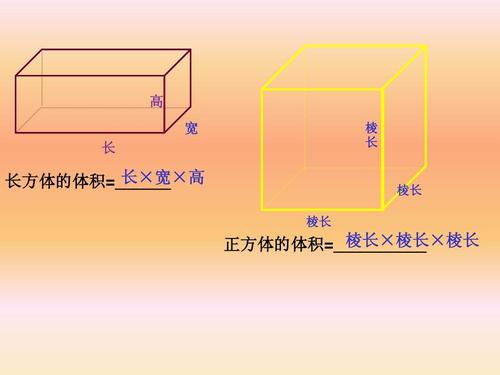
四角形の面積(「ヘロンの公式」応用) 作者 darkn さん 実行数 5192 一対の対角(の和)が判っていれば,ブレートシュナイダーの公式(Bretschneider's formula) が使えますが,ここでは「長さ情報」のみを使用しています. 辺ABの長さ考四角形の面積を2つの三角 形に分割して考え,言葉や 図,式を使って書き表すこと ができる。 表四角形を三角形に分割する 考え方を用いて面積を求め ることができる。 2 平 行 四 辺 形 の 面 5 / 12 ・三角形の面積の求め方や等積変形を「面積= 底辺 × 底辺」 すなわち 「A = s2」 例: 正方形の一辺が4㎝ (t = 4)のとき、面積はt 2 = 4 x 4 = 16 ㎠ と求めることができます。 4 対角線同士を掛けて2で割り、ひし形の面積を求めます。
四邊形 维基百科 自由的百科全书
四角形 面積 4点 座標
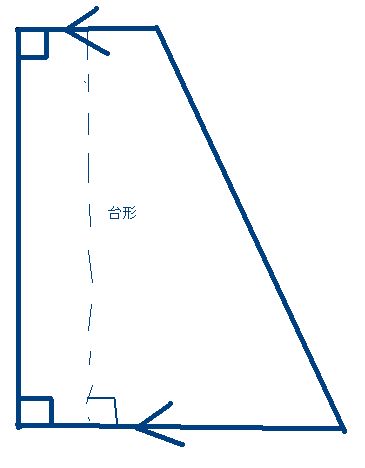
四角形 面積 4点 座標-四角形の面積の求め方(公式) 三角形に分けて面積を求める s:台形までの面積の公式はわかったけど、台形でない四角形の体積を求める公式はあるんですか? T:左の図のような四角形の面積をどうやって求めたらいいのか、ということですね。 s:そう 四角形abcdの面積は 8+75=155㎠ よって、 答え 155㎠ 例題6 下の図のような台形abcdがあります。点pは、頂点aより出発して台形abcdの辺上を秒速2cmの速さで、頂点b、頂点c、を通って頂点dまで進みます。11秒後の四角形abcpの面積を求めなさい。 解説
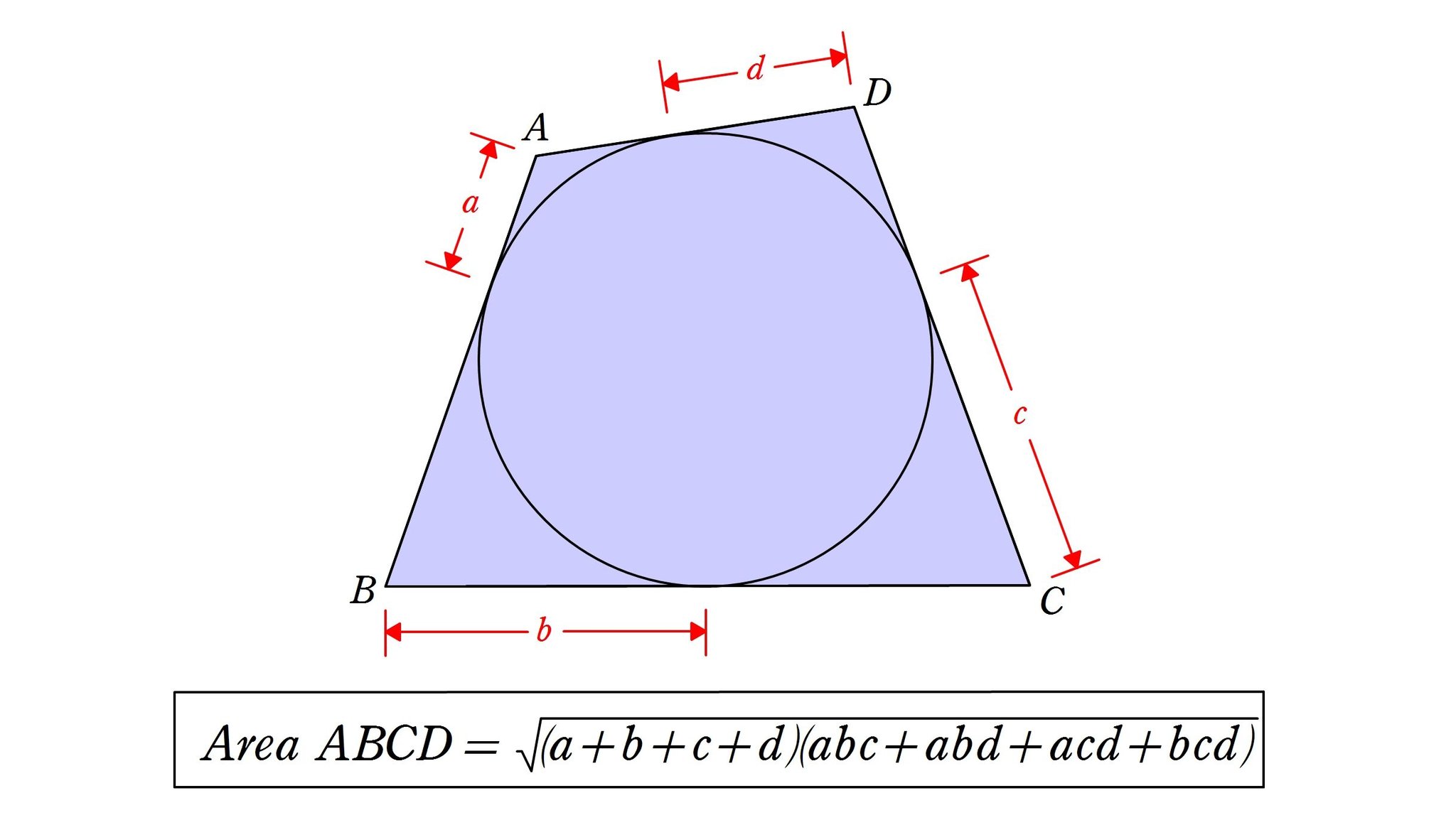



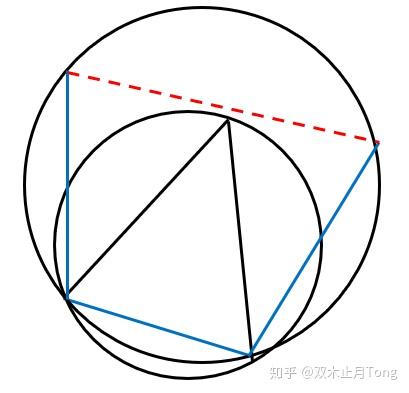
ポテト一郎 さんのツイート 円に外接する四角形の面積 なんと 角の大きさに依存しません
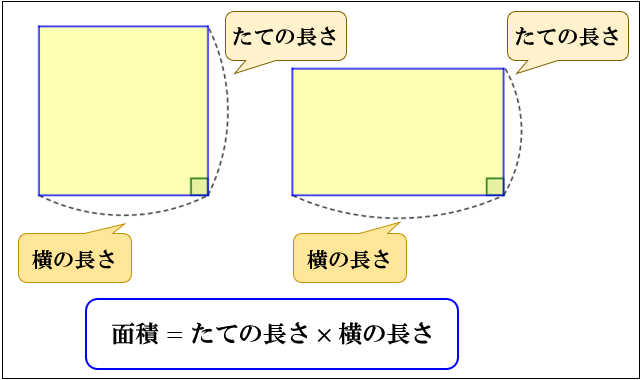
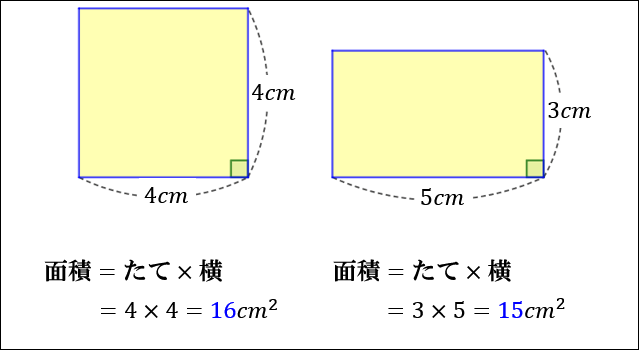
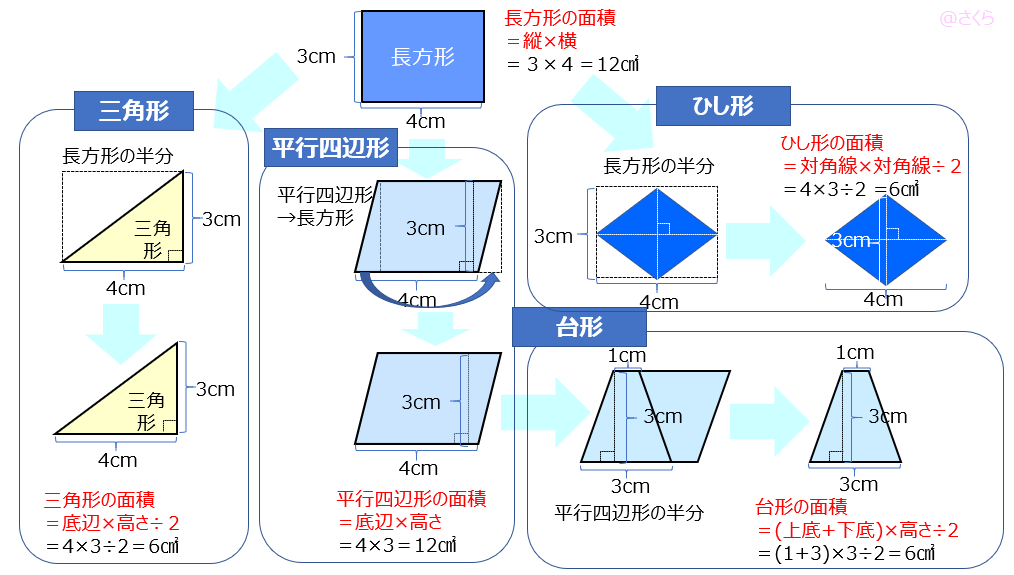
四角形の面積の計算順を守るべき理由 小学校で四角形の面積の求め方は「縦*横」と習います。 そして当然ですがこの計算結果は、順序を「横*縦」に逆転させても同じになります。 縦3cm横5cmの長方形だった場合、以下のようになります。四角形の面積を求める公式は、どれも三角形の面積を求める公式から得ることが出来ます。四角形に 対角線 (たいかくせん) を引くと、三角形に分けられますよね?四角形と三角形の面積 3 単元目標 三角形や四角形の面積の求め方を考え、説明することができる。 三角形や四角形の面積の公式を理解し、面積を求めることができる。 平行四辺形の高さと面積などの関係を調べ、比例していることを確かめる。
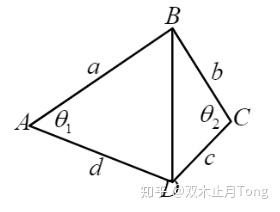
四角形の4辺と向かい合う1組の角の和から四角形の面積と周囲の長さを計算します。 正多角形の面積 正多角形の面積 正n角形の辺の長さから面積,周囲の長さ,頂点の角度,対角線の本数を計算します。 四角柱の体積=底面積×高さ =(台形の面積)×高さ = {(上底下底)×高さ÷2}×高さ となります。 つまり {(2+4)×2÷2}×3 =18㎤ この問題の答えは18㎤ということになります。 他の四角形の面積についても、これを機に復習してみてはいかが小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題
円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺フラット 円・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。1.単元名『四角形と三角形の面積』(5年生) 2.単元について 量と測定領域に関わって、第5学年の目標は、次の通りである。 (2)三角形や平行四辺形などの面積及び直方体などの体積を求めることができるようにする。ま
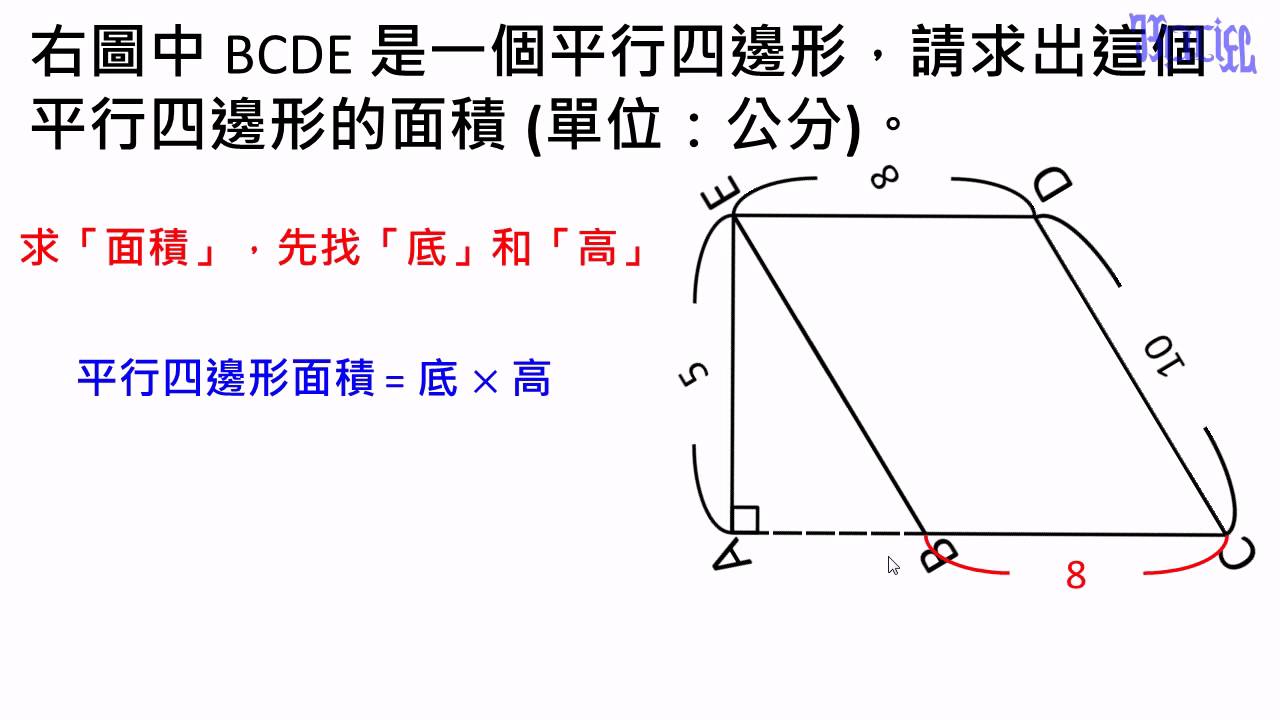



面積 33 求平行四邊形面積的進階練習 Youtube
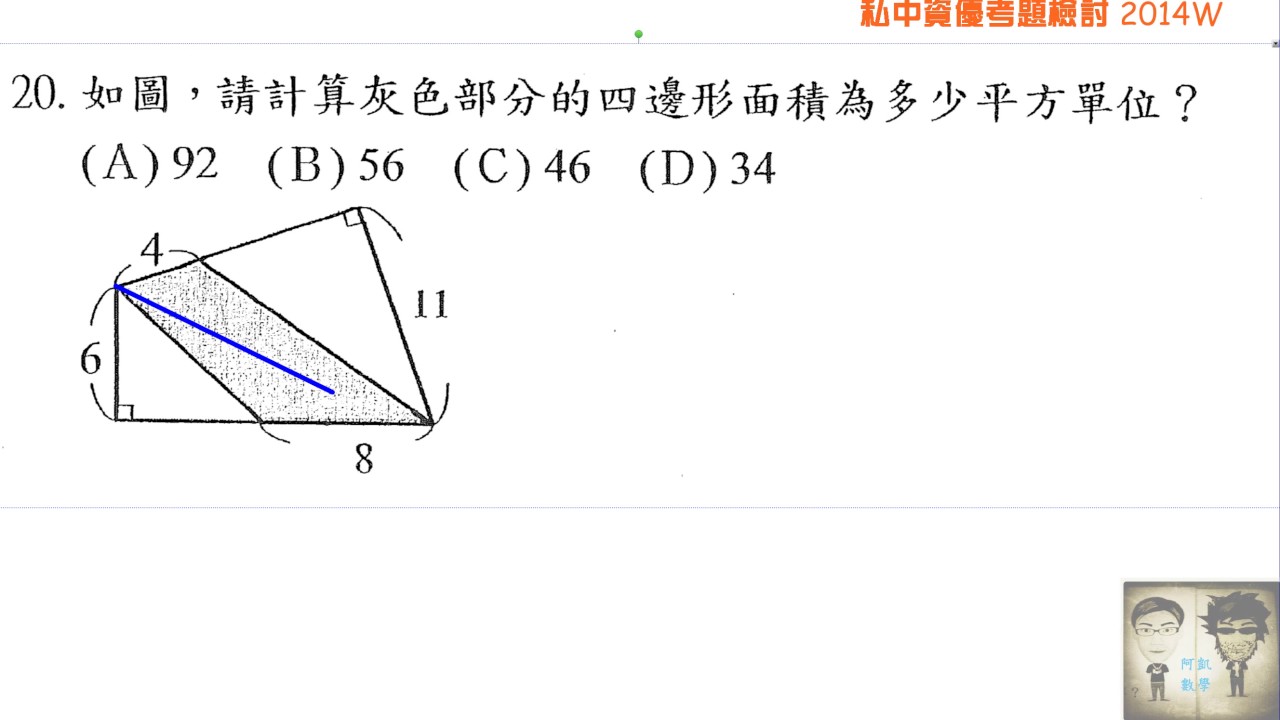



W校資優入學考題 不規則四邊形求面積問題 Youtube
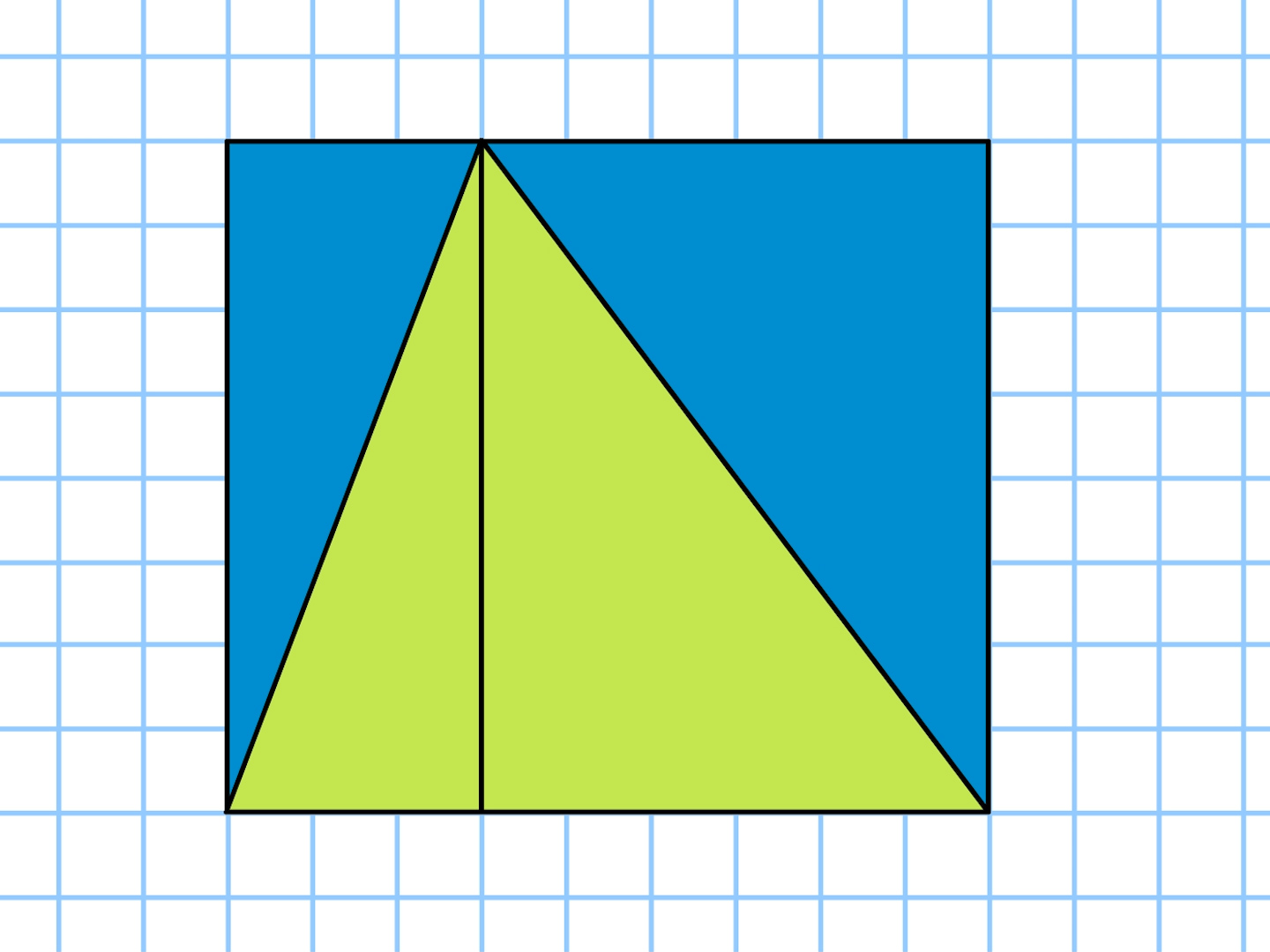
解説: 三角形ADFを3、台形ABCFの面積を5とすると、長方形ABCDの面積は8。 実際は96cm 2 なので、1で12cm 2 。 三角形AFDの面積は36cm 2 となり、 高さのDFは6cmとなり、CFは2cm。 他も同様であるから,\ 四角形{abcd}の面積は四角形{fghi}の面積の半分である S=12pqsinθは,\ 受験では{裏技公式}の扱いとなる\ 実用上は次の2点が重要である1 次の太い線の図形の面積を求める式と答えを書きましょう。 (1) (式) (2) (式) (3) (式) 13 四角形と三角形の面積 学 年 組 氏 名 11cm 6cm 10cm 7m 3m 10m ( ) ( ) 10m 9m 4m ( )



1
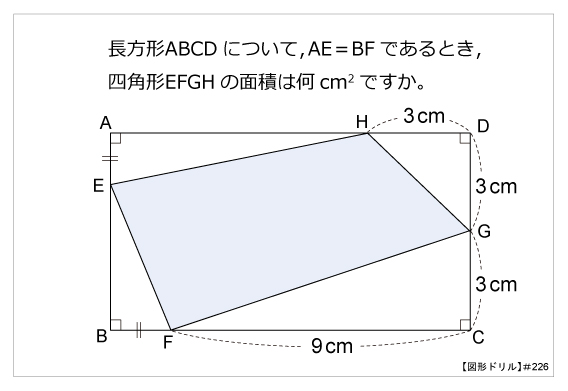



図形ドリル 第226問 長方形の中の四角形 算数星人のweb問題集 中学受験算数の問題に挑戦
長方形は縦と横で長さが違う四角形ですが、正方形は縦と横が同じ長さなので 辺×辺=面積 で求めることができます。 辺の長さが4cmの正方形の面積は? → 4cm × 4cm → 16cm 22直角四角形を,2つの三角形ア,イに分けることができました。 アの面積は,補助線よりも上の部分に書かれている長さである,「4 cm」と「8 cm」を使って,底辺×高さ÷2=4×8÷2=16(cm 2 )です。四角形に関する用語 対辺:繋がっていない(頂点を共有しない)辺のこと。四角形は2組の対辺を持つ(向かい合う辺)。 対頂点:辺を共有しない二頂点。四角形は2組の対頂点を持つ。 対角:対頂点における内角。 四角形は2組の対角を持つ(向かい合う角)。



四边形的面积公式 知乎
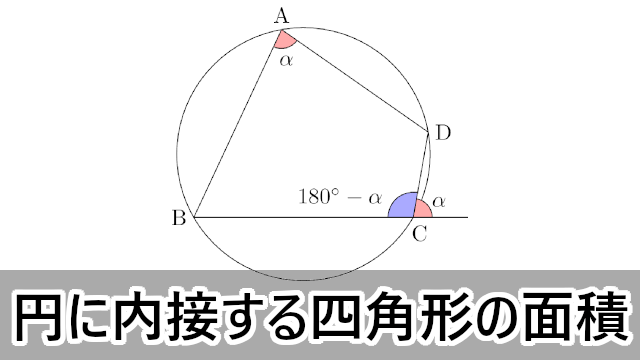



数学ia 円に内接する四角形の面積 大学入試数学の考え方と解法
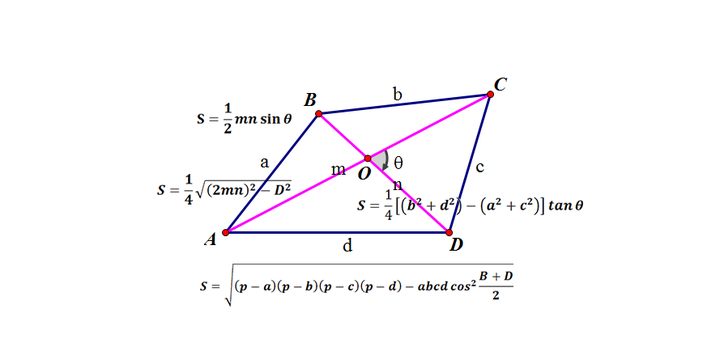
2直角四角形の面積(2) 氏名( ) ( )cm2 ( )cm2 ( )cm2 ( )cm2 ( )cm2 ( )cm2 ① ② ③ ④ ⑤ ⑥ 01立正 01共立女子 03明大付属中野八王子 01城北 01昭和女子大附昭和 04多摩大附属聖ヶ丘 12cm 11cm 6cm 18cm 4cm 4cm 65cm 2cm 4cm 5cm 6cm 2cm 4cm 7cm 5cm 2cm 3cm 5cm 4cm$3$ 辺の長さと面積がすべて整数であるような三角形を「ヘロンの三角形」(Heronian triangle)と呼ぶ「ピタゴラスの三角形」(各辺の長さがすべて整数であるような直角三角形)は「ヘロンの三角形」であるよって, $1$ 組の辺の長さが等しい $2$ つの「ピタゴラスの三角形」の等辺を貼り合わせたり 四角形の4つの辺の長さ a, b, c, d に加え、どちらか一方の対角線の長さ e が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 S 1, S 2 を ヘロンの公式 を使って求め、それらを合計することで四角形の面積を求めることができます。




4种方法来求四边形的面积



不规则四方形面积 信息评鉴中心 酷米资讯 Kumizx Com
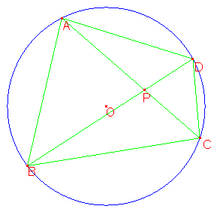
算数図形編 《面積・線分の長さ》 対称な図形を追加してみよう 理科編物質編〈ものの性質〉 温度や姿が変わると,体積と重さがどうなるか知ろう 算数図形編 《円柱・円すい・展開図・切断》 円すいが切り取られた形は相似を使おう三角形ABCの面積が85c㎡のとき、三角形ADEの面積を求めなさい。ただし、辺BCは5等分されています。 → 解答 問題5 次の直角二等辺三角形の面積を求めなさい。 → 解答 問題6 面積が0c㎡の2つの正方形が、図のように重なっています。と表せる。内接円を持つ四角形の性質とブラーマグプタの公式を利用して得られる簡潔な公式である。 さらに一般化して円に内接しない四角形の面積を求める公式も知られている。四角形 abcd の対角の和、たとえば ∠abc ∠cda の半分を t とすると
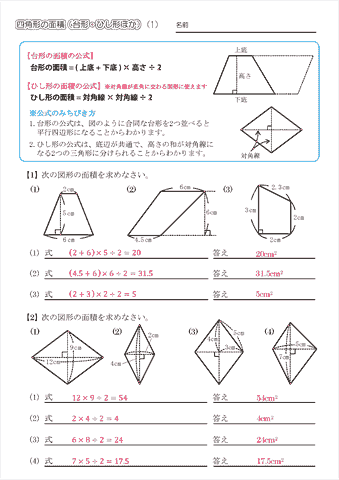



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生




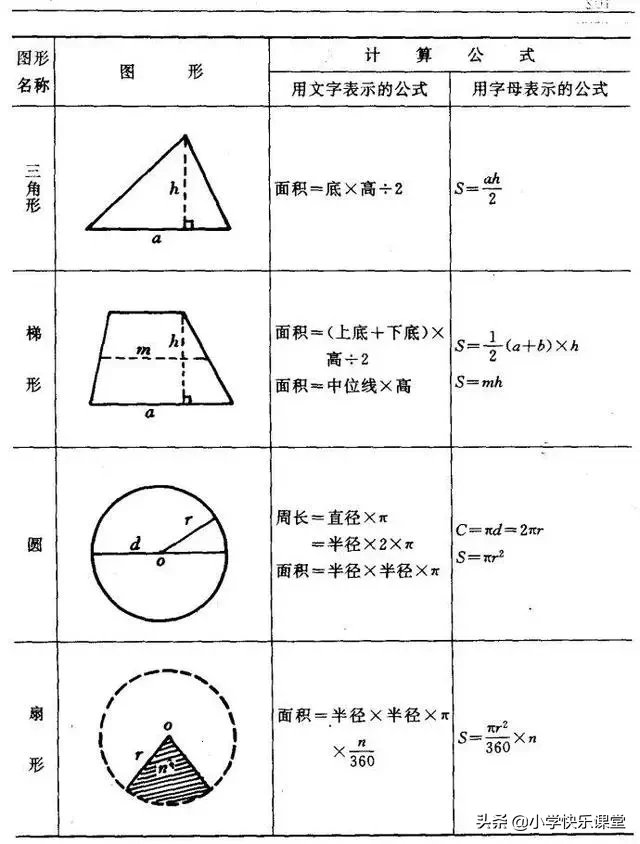
面積の求め方 計算公式一覧
四角形の面積の計算順を守るべき理由 小学校で四角形の面積の求め方は「縦*横」と習います。 そして当然ですがこの計算結果は、順序を「横*縦」に逆転させても同じになります。 縦3cm横5cmの長方形だった場合、以下のようになります。 縦×横:3 * 5 = 15三角形adeと三角形ebcは相似なので、面積の比は4:9。 de:eb=2:3なので、三角形aedの面積:三角形aebも2:3。 三角形aedの面積を4とすると、 三角形abe=6、三角形ebc=9、三角形dec=6になる。 台形abcdの面積は4+6+9+6=25。正方形・長方形 面積問題④ 小学4年生 計算無料プリント 算数問題 小学生で学習する正方形・長方形 面積 問題です。無料プリントなので、是非ダウンロードしてお使いください。算数計算問題プリン 記




4种方法来求四边形的面积
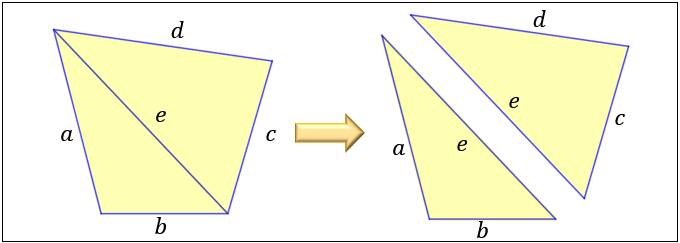



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
計算バグ (入力値と間違ってる結果、正しい結果、参考資料など) 説明バグ (間違ってる説明文と正しい説明文など) アンケートは下記にお客様の声として掲載させていただくことがあります。 円に内接する四角形の面積(4辺から) にリンクを張る方法 ワークシートを見直して、書き換えました。 5年 四角形と三角形の面積(表紙) 5年 四角形と三角形の面積(ワーク特に,相似な三角形の面積比は相似比の二乗に比例することも分かります。 →相似比と面積比,体積比の公式の証明 また,サインの性質: sin θ = sin (18 0 ∘ − θ) \sin \theta=\sin (180^{\circ}\theta) sin θ = sin (18 0 ∘ − θ) に注意すると,円に内接する四角形



2直角四角形の面積を求める極意 すぐるゼミ
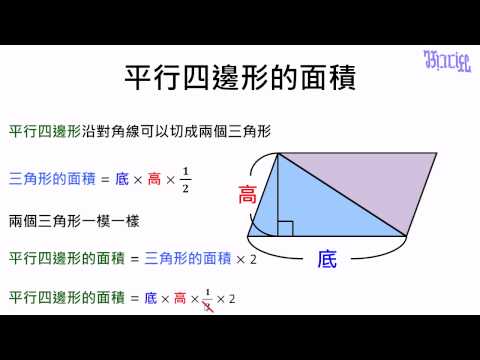



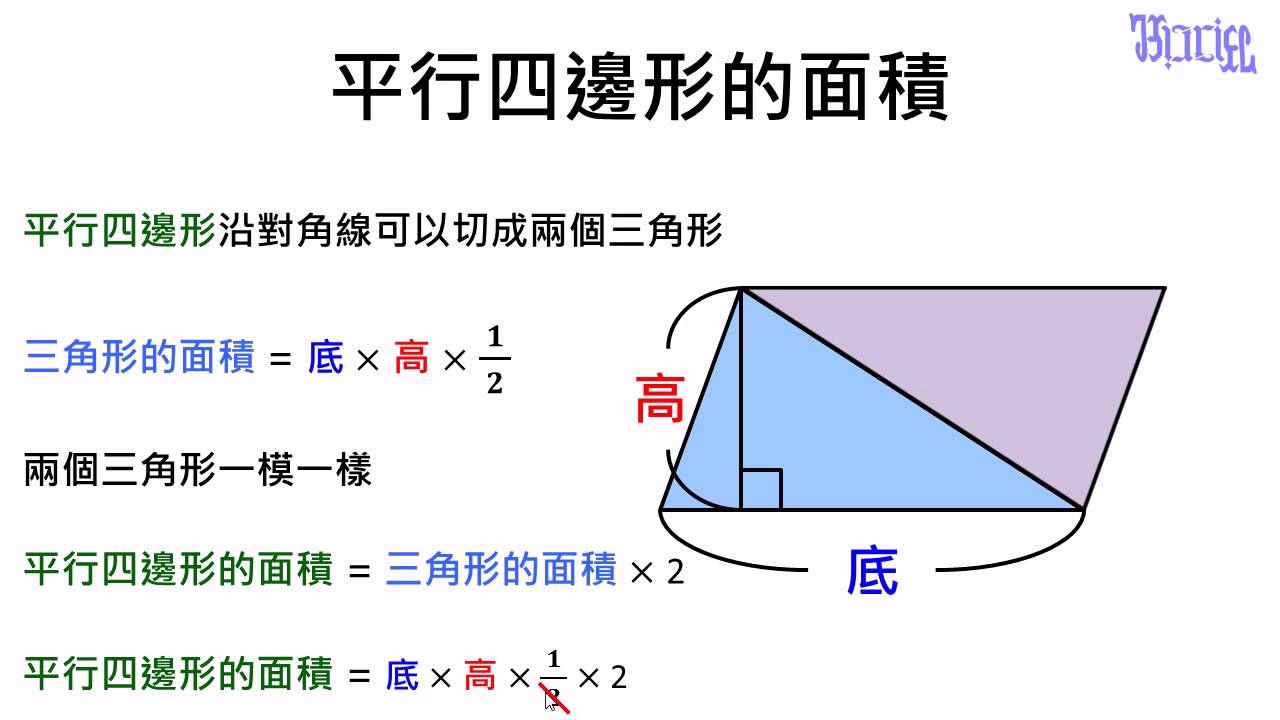
觀念 平行四邊形的面積計算方式證明1 數學 均一教育平台
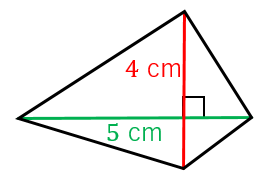
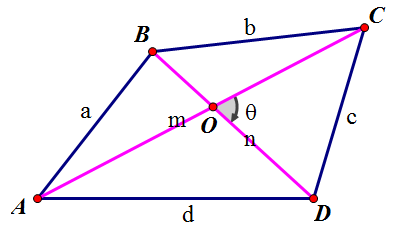
を結び四角形を分割したら、左図のよう な面積となった。このとき、 四角形PLCMの面積を求めよ。 この問題に対して、右図のような補助線を引いて考えることがポイントとなる。四角形の2本の対角線の長さを a, b 対角線の交わる角度を θ としたとき、四角形の面積 S は、 S = 1 2 a b sin θ 式B である。 ことが分かる。 ということで、問題を解こう。 式Bより、問題の四角形の面積 S は、 S = 1 2 ⋅ 5 ⋅ 4 sin
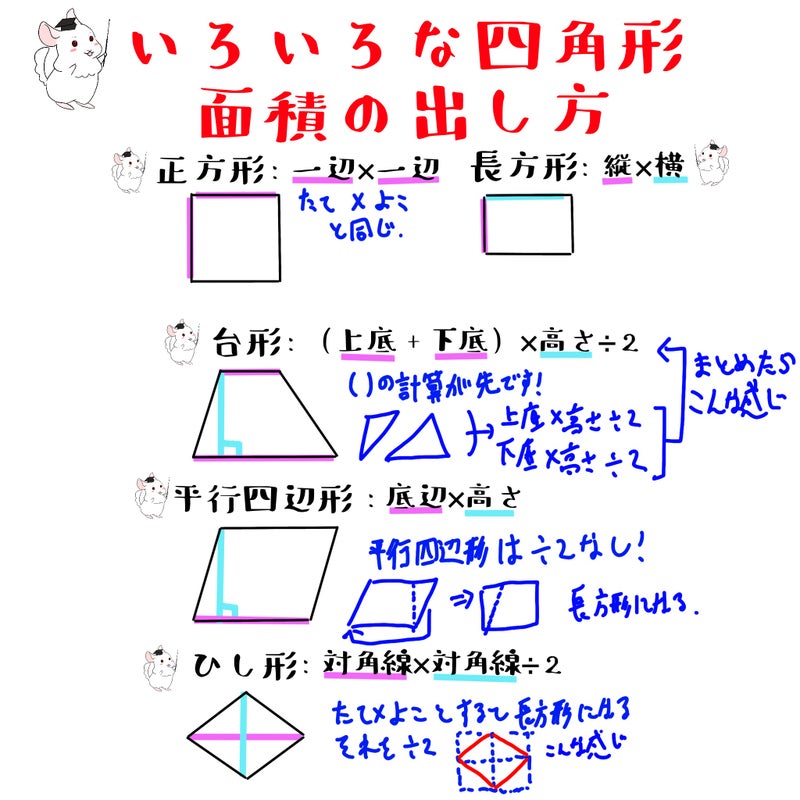



四角形の面積について 小5 小6 中1 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生




菱形面積公式證明ひし形の面積の求め方 Tzpage



1



File Bousi1 Jpg Wikimedia Commons




4种方法来求四边形的面积
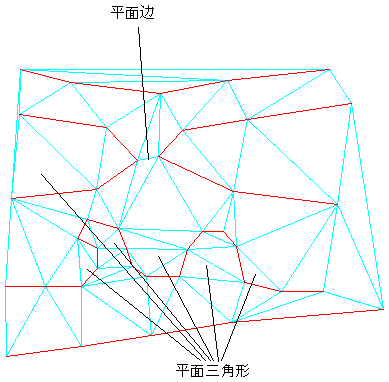



关于最小化曲面中的平面面积 Autocad Civil 3d Autodesk Knowledge Network
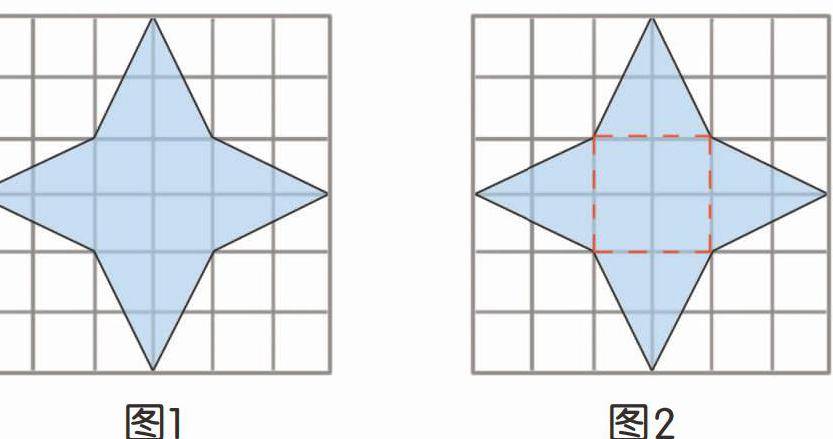



格点多边形遇上毕克公式 参考网



7 4 平行四邊形的面積公式 高市資教中心教材網



Q Tbn And9gcshxxcmn2t9uovv2aaxth Adgnpsliblch Z A5j3glszyobejd Usqp Cau




平行四边形面积 周长 对角线在线计算器 三贝计算网 23bei Com



面積最大の四角形
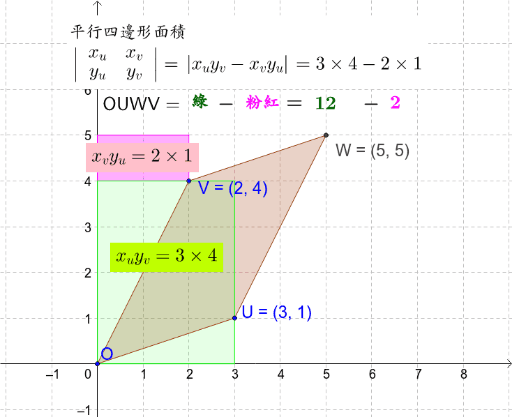



行列式計算平行四邊形面積 Geogebra




Pdf Values In Japanese Mathematics Education From The Perspective Of Open Ended Approach Semantic Scholar




4种方法来求四边形的面积




六角形面積公式正六邊形 Utvos



四邊形 维基百科 自由的百科全书



八角形面積計算八角形面積公式 百度知道狀態 Ekcup




正六角形三角形小學數學三角形的特性知識點大全 Vnfp




等腰梯形 维基百科 自由的百科全书
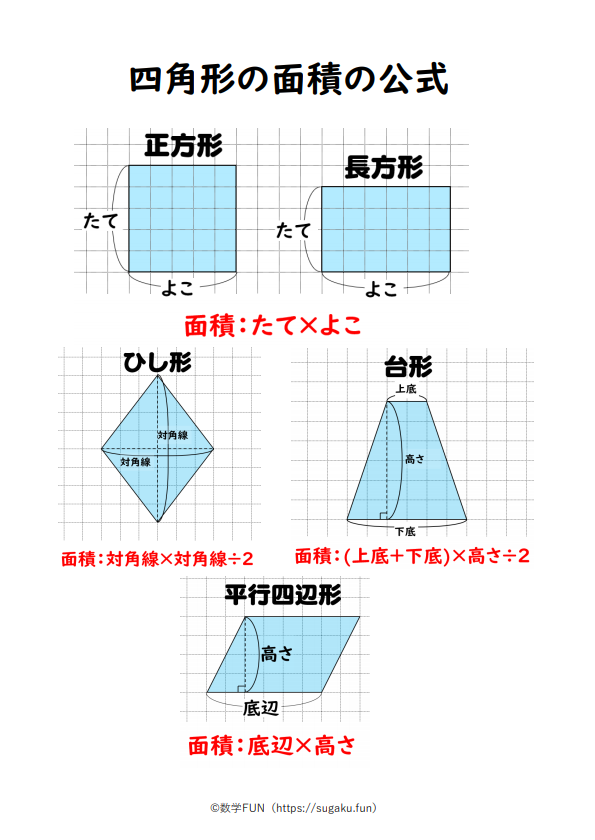



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
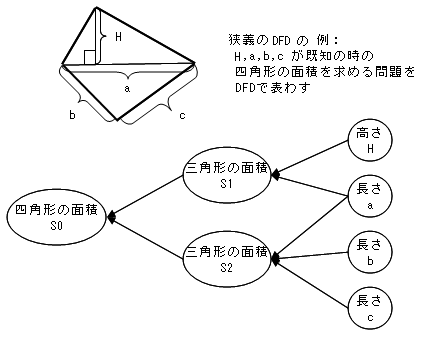



File Pure Data Flow Diagram Example Png Wikimedia Commons



三角形 四角形の面積比 中学から数学だいすき
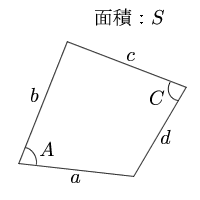



四角形 4辺と対角の和 面積の計算 計算サイト



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学



この四角形の面積の求め方を教えてください 難しいことを考えず普通に考 Yahoo 知恵袋



国际数学竞赛 四边形面积公式知多少 知乎




4种方法来求四边形的面积




四邊形 维基百科 自由的百科全书



正方形面积公式



只用一刀 将一个四边形切成面积相同两部分 这方法值得一学 网易视频




八角形面積計算八角形面積公式 百度知道狀態 Ekcup



四角形の種類と面積の求め方 算数勉強会 小学 楽天ブログ




六角形面積公式正六邊形 Utvos
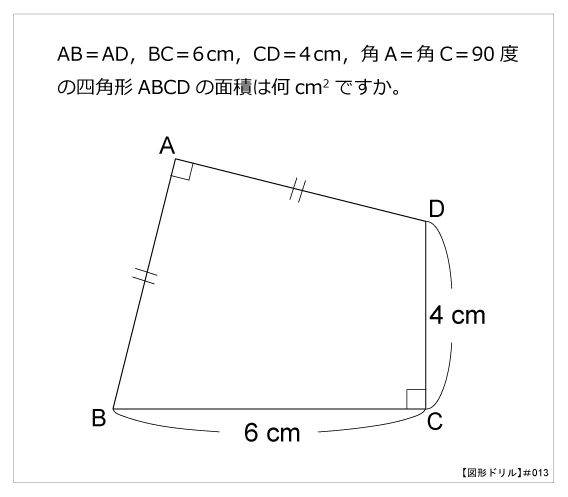



図形ドリル 第13問 四角形の面積 算数星人のweb問題集 中学受験算数の問題に挑戦



松本市学研梓川教室やまと教室公式ブログ 四角形の面積の公式
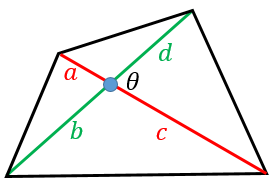



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学




四边形面积
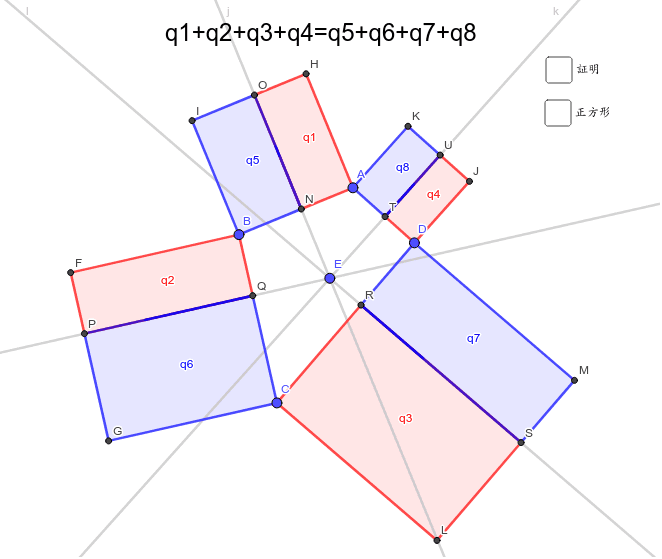



垂線の性質 四角形面積の等分 Geogebra




4种方法来求四边形的面积




4种方法来求四边形的面积
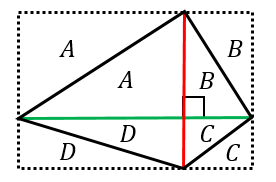



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学



四角形の面積




ポテト一郎 さんのツイート 円に外接する四角形の面積 なんと 角の大きさに依存しません



正方形面积公式




この四角形の面積を求めると 18 3 になるらしいんですけど 求め方を 高校 教えて Goo




四角形の対角線と面積 数学i フリー教材開発コミュニティ Ftext



四角形と面積比 べっこう色の記録
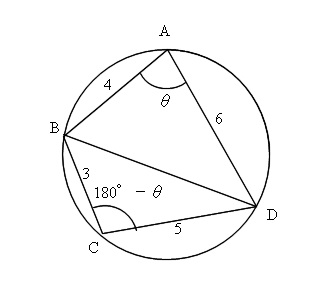



円に内接する四角形の面積の求め方と定理の使い方




小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生



7 4 平行四邊形的面積公式 高市資教中心教材網



技巧 数学图形面积计算的十种方法 正方形




不規則圖形面積計算 每天10分鐘 奧數一點通 每日頭條




図形 三角形 四角形から面積 体積の計算まで くもんのまんが算数シリーズ 2 Hitoshi Ogino Kentaroi Miura Amazon Com Books
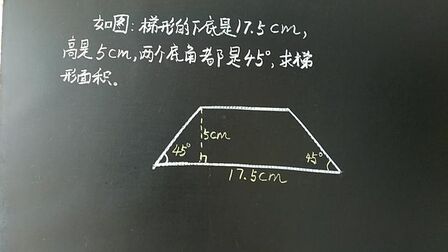



不等边梯形面积计算公式 搜狗搜索
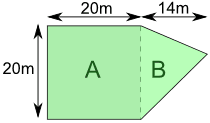



圆形 三角形 正方形 矩形 平行四边形 梯形和扇形的面积



四边形的面积公式 知乎



国际数学竞赛 四边形面积公式知多少 知乎



圆内接四边形 维基百科 自由的百科全书



面積 Blaise



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



面積 04 平行四邊形的面積計算方式證明1 Youtube
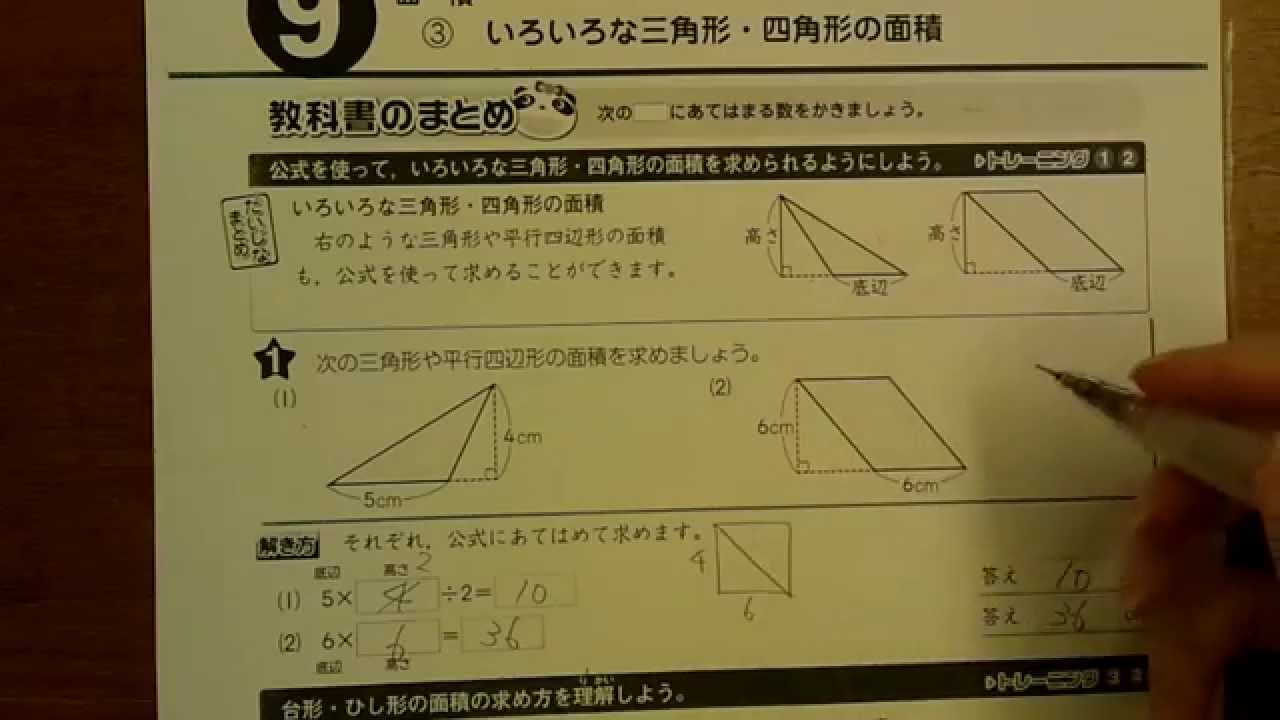



算数5年 3 いろいろな三角形 四角形の面積例題p 74 Youtube




不平行四边形面积计算公式与在线计算器 三贝计算网 23bei Com



四边形的面积公式 知乎




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




円に内接する四角形の面積をサインを使って求める問題 数学i By ふぇるまー マナペディア




4种方法来求四边形的面积




4辺が与えられたとき 面積最大になる四角形は 身勝手な主張



數學漫畫系列2 圖形 認識三角形和四邊形到面積與體積的計算 讀書共和國網路書店




不等边四边形面积计算公式与在线计算器 三贝计算网 23bei Com
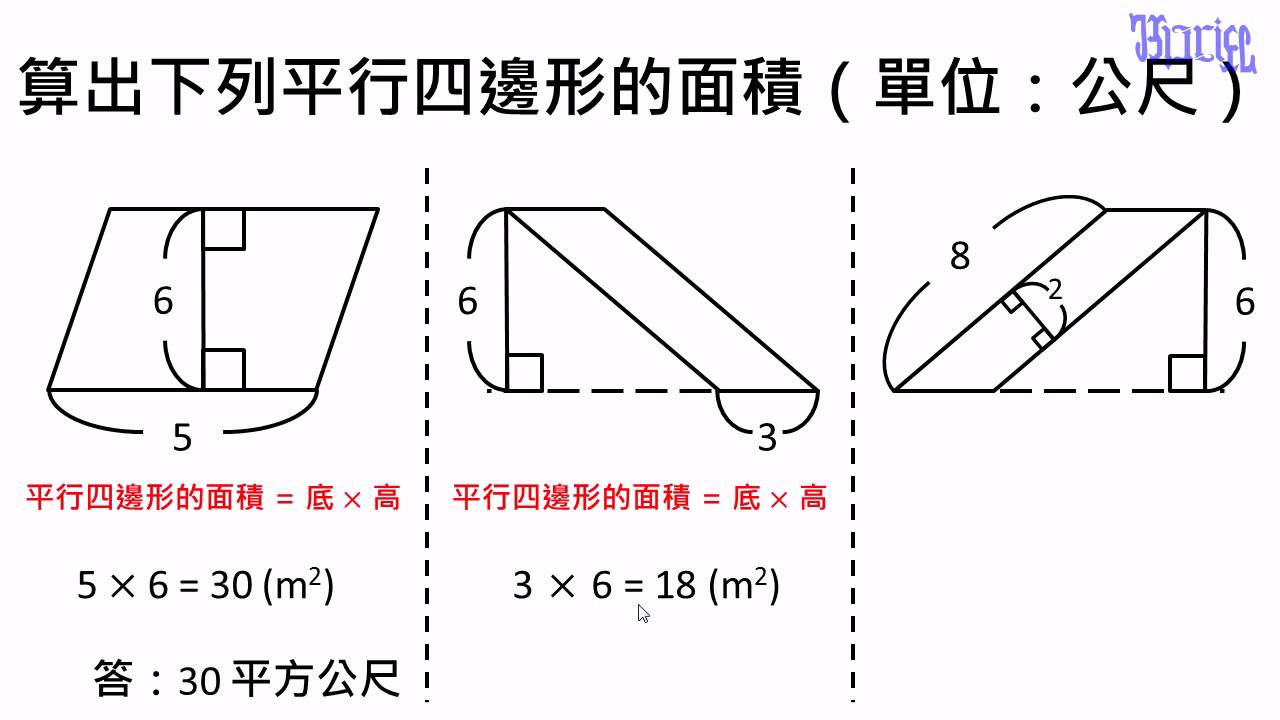



面積 06 平行四邊形面積的基本計算題 Youtube




四边形面积
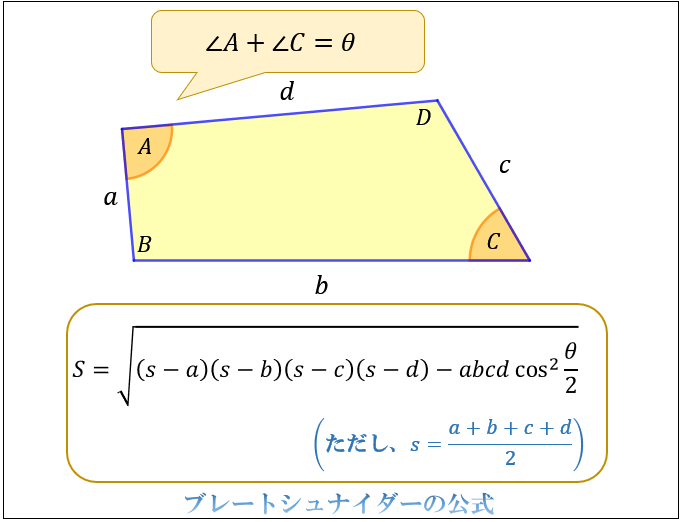



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




4种方法来求四边形的面积



四角形の面積を求めたいとき 4辺の長さが分かっているだけでは面積を Yahoo 知恵袋



四角形の面積を4辺から求める 面積計算機
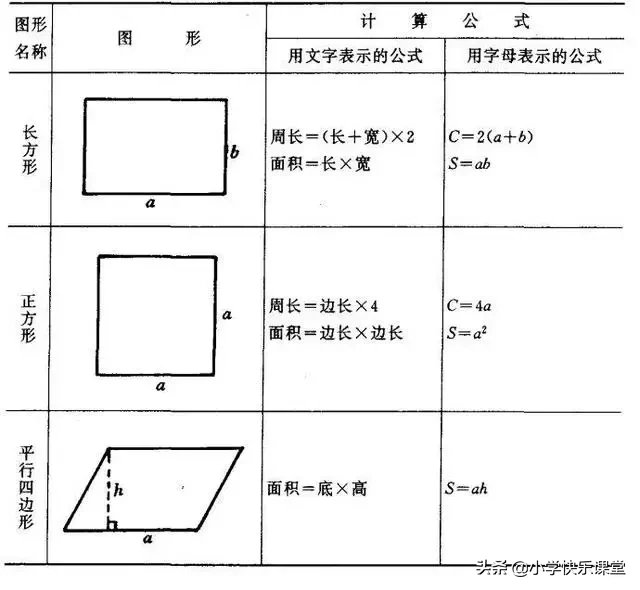



正方形面积公式



四角形の面積 ヘロンの公式 応用 高精度計算サイト




和角公式幾何證明 證明 L 差角與和角 Lhlv




如何找到平行六面体的侧面面积 数学21



正方形面积公式



1




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




高校数学テクニック集 002 数学 A 三角比 四角形の面積を求める公式 大学受験対策 数学i 図形と計量 学習塾 Dear Hope ディアホープ 改訂 Youtube




4种方法来求四边形的面积



対角線と四角形の面積 図形と計量 おおぞらラボ



四角形の種類と性質 面積の公式について 中学受験 ゲーム大好き息子の偏差値32からの挑戦




正方形面积公式



不规则图形面积计算十大法则
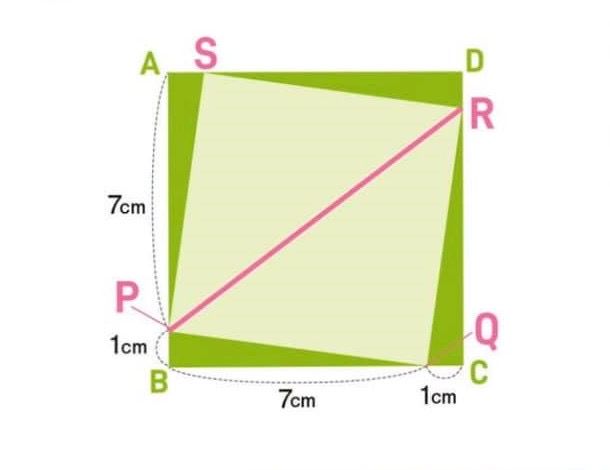



小学校で習う 四角形の概念 と 面積の公式 だけ で解いてみよう 解答編 Npo Selfish セルフィッシュ



0 件のコメント:
コメントを投稿