10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 p 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り( 5 − 3)!27/7/ さあ、この問題は「順列」か「組み合わせ」かどちらでしょうか? 答えは 「 順列 」 です。 委員長・副委員長・書記を選ぶことは、10人の中から3人選んで並べることと同じであると考えら
数学i Aチェック リピート 第7章 2順列 組合せ 8 同じものを含む順列 Pukiwiki
順列 組み合わせ 問題 違い
順列 組み合わせ 問題 違い-中学受験 5年 unit 71 場合の数1 順列と組み合わせ1 例題と解説 トレーニング 確認テスト ログインが必要です 関連する過去問 4年生向け 市川中学校06 場合の数= 5 × 4 × 3 × 2 × 1 3 × 2 × 1 × ( 2 × 1) = 10




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学
順列・組み合わせで解けるけれど,どう解いてよいのか迷う人が多そうな問題を集めてみました。すべて「順列作戦」と「組み合わせ作戦」の2通りの解法を用意してありますので,頑張って挑戦してみてください。例題1 \(aaabb\) の並べ替え ★例題19/2/21 順列と組み合わせの練習問題 見分け方のポイント、「順番に並べるか」「順番を変えると意味が変わるか」に注意しながら、練習問題に挑戦しましょう。 練習問題①「3 役を選ぶ」数学・算数 順列・組み合わせの問題です。 順列・組み合わせの問題です。 0,1,2,3,4の数字から異なる3個の数字を取ってできる3桁の整数は全部でいくつですか? という問題ですが、 一の位は5 質問No
この問題の場合, a から b へ最短で進むには必ず右に 6 回と上に 5 回進むことになるので, 「右に進む」 6 個と「上に進む」 5 個を並べる順列の数が,最短経路の総数になります。 よって,同じものを含む順列の考え方から (通り) となります。この計算で整数を作る問題難しい 以上 $3$ つを解説します。練習問題 10 人の生徒がいます。 以下の問に答えよ。 (1) 3 人を選ぶとき何通りの選び方がありますか。 (2) 8 人を選ぶとき何通りの選び方がありますか。 練習問題 解答へ 数学aの目次へ 数学の
順列・組合せ総合問題 練習問題19 5人の旅客が3件の旅館に泊まる泊まり方は何通りあるか。 ただし1人も宿泊しない旅館があってもよいとする。 上の問題において,人を仮に固定し,どの旅館に宿泊するか,ということを考えればよいのです。 発想の( 3 − 2)!例題 (1) 両親と子供 4 人の 6 人が円形のテーブルに向って座るとする。 次のような座り方は何通りあるか。 ( ア ) 6 人全体の座り方 ( イ ) 両親が隣り合わない座り方 ①異なる n 人 ( n 個 ) を並べる円順列は で求めよう。 ②隣り合わないときは余事象,または間に入れよう。 (1) ( ア ) 6 人の円順列の総数より ( 通り )




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




順列と組み合わせ 問題と解決策を含む完全な概要 Lambdageeks
トップページ > 適性検査・筆記 > 頻出問題7:『順列・組み合わせ』 頻出問題7:『順列・組み合わせ』 出題傾向と問題の概要 テストセンターで出題可能性のある問題です。 組み合わせ問題12(組み合わせ) 問題21(少なくとも) 問題22(少なくとも) 問題31(順列) 問題32(順列) 問題41(円順列) 問題42(円順列) 問題51(同じ物を何回使ってok) 問題52(同じ物を何回使ってok) 問題6(コインの裏表) 問題7(配り方) 問題8(図形の塗り分け)両者を見比べたら分かるかと思いますが、 選んだものに順番や役割を与えて区別する のが 『ならべ方』 の問題で、 ただ選ぶだけ なのが 『組み合わせ』 の問題です。 では具体的にそれぞれの問題を解いてみましょう。 ならべ方・組み合わせの問題の解き方




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




順列と組み合わせ 算数用語集
10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 P 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り 例 2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から重複を許して2つを取って並べる順列 10Π2 =10 2 =100 のうち,先頭が0のもの(10個)は1桁になるか では場合の数、順列と組み合わせの応用問題5問を試してみましょう。 「順列と組み合わせ」の応用問題: 問題 1―1: 野球チームの地区同士の優勝決定戦がある。東地区代表のチームaと、西地区代表のチームbが対戦し、先に4勝した方が優勝となる。= 3×2 ×1 2× 1× (1) = 3 3 C 2 = 3!




Spi対策 順列と組み合わせ 並び方 練習問題




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
= 5 ×4 ×3 ×2 ×1 3× 2× 1× (2 ×1) = 10 5 C 3 = 5!15/6/ spi対策順列と組み合わせ① 並び方 spi spi対策時間と距離と速さ① 練習問題 前回学習した時間と距離と速さの練習問題です。今回は全部で2問。あなたは何問解けますか? spi年 駒澤大 仏教・文・経済・法 1 (1) 上の問題文をクリックしてみて下さい. 順列の基本問題です. 偶数となる整数は一位の数字が2か4のいずれかです.



Q Tbn And9gcsvqfv2gklhrmh2 X2wsifj7ext7jpqr Kj8n7lb0b6jvmqux1p Usqp Cau



2
22/1/18 組合せとは いくつかのものからいくつかのものを取り出して 並べる ことを 順列 と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は 組合せ の問題と呼ばれています. 順列 → → 順序を考慮練習問題 練習問題+解答 組合せの総数 n C r が整数であることの証明確率 例題(8) 練習問題 練習問題+解答整数の性質 例題(11) 練習問題 練習問題+解答図形の性質 例題(18) 練習問題 練習問題+解答 三角形の角の二等分線と比 メネラウスの定理,チェバの定理順列と組み合わせの例題をいくつか紹介していきます。 例題 (順列) 4つの整数1,2,3,4から異なる3個を取り出して並べるときの3桁の整数の数。 解答 4つの整数から異なる3つを取って並べて出来る3桁の整数は \(_4 p_3 =4⋅3⋅2=24\) よって24通りです。 例題 (組み合わせ)



1



数学a 順列と組み合わせの違い 無料問題付き 平野雅人のブログ
spi問題形式2:順列・組み合わせ ・順列・組み合わせ(並べ方と選び方) ある野球部の部員は、男子5人と女子3人の8人である。 (1)この8人の中から、部長と副部長を1人ずつ選びたい。選び方は何通りあるか。 a 14通り b 28通り c 56通り27/4/19 問題 男子3人、女子4人が1列に並ぶとき、次のような並び方は何通りあるか。 (1) 両端が男子である (2) 女子4人が続いて並ぶ (3) 男子、女子が交互に並ぶ ある種、順列の典型問題ですので、これを通して順列の問題の考え方を学んでください。問題32(順列) 問題41(円順列) 問題42(円順列) 問題51(同じ物を何回使ってok) 問題52(同じ物を何回使ってok) 問題6(コインの裏表) 問題7(配り方) 問題8(図形の塗り分け) 問題9(図形の塗り分け) 最速解法&例題




順列 組み合わせ 階乗とは わかりやすくまとめてみた 数学 もんプロ 問題発見と解決のためのプログラミング



至急 Spiについて質問です 順列 組み合わせ この問題 Yahoo 知恵袋
つまり、 順列では、並べる順序を問題にして考えますが、組合せでは順序を 問題にしないで取り出し方だけを問題 にして考えます。 したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶたとえば 3 つの要素から 2 つを取り出す組み合わせなら、以下のように計算できます。 3C2 = 3!組合せ数学(くみあわせすうがく、英語 combinatorics )あるいは組合せ論(くみあわせろん)とは、特定の条件を満たす(普通は有限の)対象からなる集まりを研究する数学の分野。 離散数学の中核の一つとされる。特に問題とされることとして、集合に入っている対象を数えたり(数え上げ的




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



spi頻出問題7 順列 組み合わせ
= 3 × 2 × 1 2 × 1 × ( 1) = 3 さらに、5 つの要素から 3 つを取り出す組み合わせなら、以下のようになります。 5C3 = 5!同じものを含む順列の応用問題3選 では次に、同じものを含む順列の応用問題について考えていきましょう。 具体的には、 隣り合わない文字列の問題;1/3/ SPI 場合の数 順列・組み合わせの基礎 この単元の基礎は分量が多いです。 頑張って学習しましょう! ! 1 PとCの使い分けの解説です。 <問題> 1~3のカードが1枚ずつある ① 2けたの整数は何通りできるか ② 2枚選ぶのは何通りあるか




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
16/6/ spi対策順列と組み合わせ③ 余事象 今回もまたイベントに向けてアルパカを選んでいるようですが、少し条件が難しいようです。 一番適切な数のアルパカを選ぶいい方法は何かないで解答と解説 『順列・組合せ』の問題の解き方や、使う公式に関しては『spi 順列・組合せ ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。17/3/21 ☆問題のみはこちら→順列と組み合わせの解法パターン(問題) ①約数に関する問題でまずすることは? →素因数分解 ②p⁰ →=1 ③条件が複数ある場合の数を考えるときはどのような条件から考えるか? →条件が厳しいものから順 "順列と組み合わせの解法パターン(問題と答え)"の続き



確率基礎問題 Of 京極一樹の数学塾会員頁




順列と組み合わせの公式とその違い 問題付き 理系ラボ
順列組合せにおける「割り算」の意味について 順列組合せの問題で「割り算」を使うことがよくあります。 例えば、 などなど。 いずれも「割り算」を行っていますが、その意味を正しく理解しているでしょうか? まずは、以下の小学生レベルの問題にでは、 順列と組み合わせの簡単な見分け方 を紹介します。 見分け方の1つは、 問題文のなかで"並べていたら"順列、"選んでいたら"組み合わせ です。 問題文のなかに、並べるというワードがあれば順列で順列と組合せの応用問題5選 それでは、ここからは順列と組合せの応用問題をごちゃまぜに $5$ 問解いていきたいと思います。 具体的には 委員の選出;
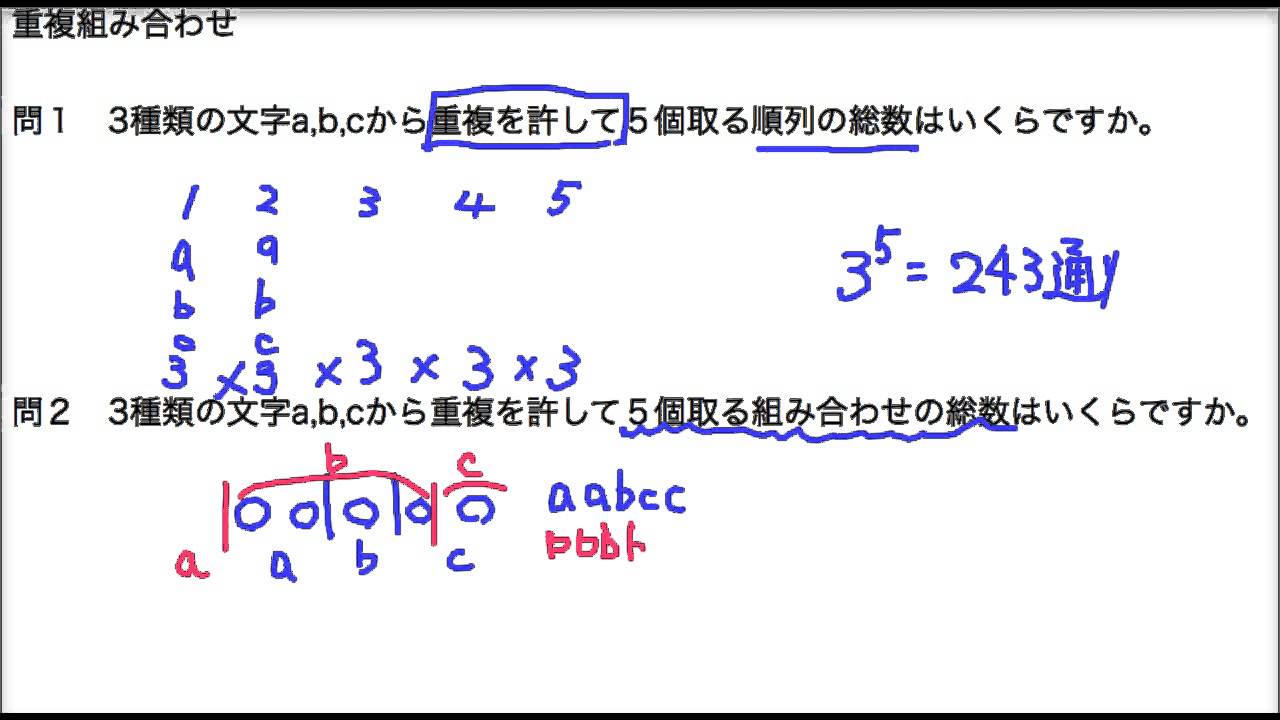



重複組み合わせ1 順列と組み合わせの違い Youtube




順列の問題 一定の条件で並べる 高校数学の知識庫
問題文を図で表すと、下図のようになります。 \(\\\) \(\\\) 問題は、(2)とよく似ていますが、選んだあとに1列に並べないといけません。 つまり、「順列」の考え方も必要となります。 まず、8人中、男子3人、女子2人選ぶ総数は、(2)より \(\\\) \begin{eqnarray}Spi 順列と組み合わせの問題の解き方説明 SPIの順列・組み合わせの問題は、他のSPIの問題と異なり、もう高校レベルの知識が必要になります。 このページを見る人の半数以上は、大学受験に数学を使ったきりでそれから3年以上数学に触れていない可能性も 考えられます。前回 https//wwwyoutubecom/watch?v=gkeQK_kfa5w 次回 https//wwwyoutubecom/watch?v=4LJtn7VG67Mサブチャンネル とある男がゲームを




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




ハヤト 勉強垢 Spi対策 0 59 07 不正解問題 5月8日 非言語 12 順列 組み合わせ 重複 円 応用 問題87 問題91 普通にキツすぎ 公務員試験の順列組み合わせはサクサク出来るのにspiの順列組み合わせは壊滅的 ハヤトの勉強報告 T Co
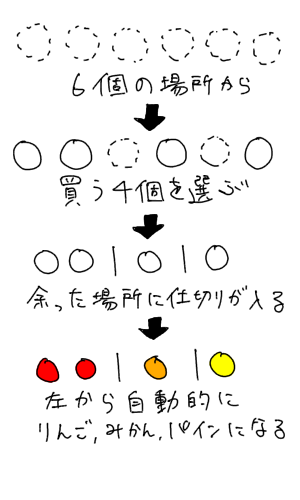



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書



数a順列組み合わせ 2番と3番の問題について なぜ分数になる Yahoo 知恵袋




重複順列と重複組み合わせの問題はどうやって見分ければいいですか Clear




組み合わせの考え応用 最短経路選択問題をシミュレーターで理解しよう 数学入門




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



順列 組合せランダムチェック公開 現役講師が作った使えるサイト




順列と組合せの違いと例題 高校数学の美しい物語




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学



順列組み合わせの問題教えてください 画像の問題どちらもわかりません 1番は9 Yahoo 知恵袋



3




Spi 非言語問題 順列 組み合わせの応用 就活の答え




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




この問題はなぜ順列の公式ではなく 組み合わせの公式で説いているのですか Clear



Spi M54e217p7lcis9d Com Jyunretu Kumiawase Q1




北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭



重複組合せ



数学i Aチェック リピート 第7章 2順列 組合せ 8 同じものを含む順列 Pukiwiki




高校数学a 組合せの基本と順列との関係 Ncrの性質 受験の月
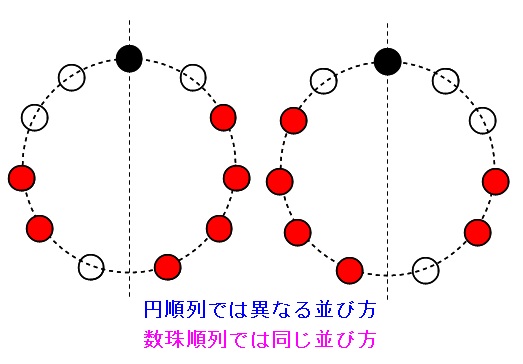



円順列と数珠順列の考え方や公式と問題の解き方




リンゴ9個 重複組合せ 解説その1 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



数学i Aチェック リピート 第7章 2順列 組合せ 10 最短経路 Pukiwiki



同じものを含む順列の問題 京極一樹の数学塾




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説




Spi 数学 対策問題 組み合わせ 順列 しかくのいろは




原田 浩明 Sサクシード223 組に分ける問題 同じものを含む順列 高校 数学 数a 組合せ



Spi順列組み合わせの問題なんですけど この問題の解法ってcやpや を使わな Yahoo 知恵袋




Spi 場合の数 最速解法 例題 Study Pro Spi




順列組み合わせ 気候の問題 高3センターファイナルから 予備校講師 みはらっち0 0 のオフィシャルなブログ




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




重複組み合わせをわかりやすく解説 公式を使えない問題も攻略しよう みみずく戦略室



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




重複順列とは 重複順列の公式と使い方




3講 順列 1章 場合の数と確率 問題集 高校数学a




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




順列と組み合わせの公式とその違い 問題付き 理系ラボ




順列 組み合わせ 問題は 子供達は大好きです イメージ図で簡単に解けるんです 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます




15年10月 怜悧玲瓏 高校数学を天空から俯瞰する




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




高校数学a 組分け問題全パターン 受験の月




順列pと組み合わせcの違いと 簡単 な見分け方




北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭




重複組合せ 組合せ 重複順列に関する問題 2018年度前期日程高知工科大学の入試問題 身勝手な主張




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube



同じものを含む順列の問題 京極一樹の数学塾




順列と組み合わせの公式とその違い 問題付き 理系ラボ



同じものを含む順列の問題 京極一樹の数学塾




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学




場合の数19 円順列と数珠順列 怜悧玲瓏 高校数学を天空から俯瞰する
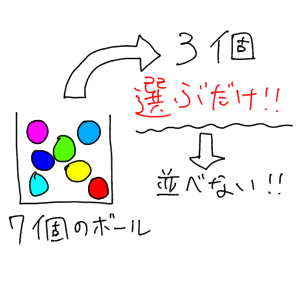



組み合わせ 並べない順列のこと 考え方と計算方法を解説 理数白書
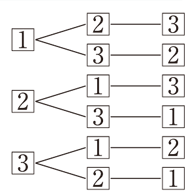



順列と組み合わせ 算数用語集




場合の数 重複組合せ と 重複順列 の違いをわかりやすく解説します



場合の数 学び家 Com




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




苦手でも分かる 順列 P と組み合わせ C の使い分け 確率 ともよし塾 受験と科学の解説授業




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




基本問題 場合の数6 同じものを含む順列と重複組み合わせ 同じものを含む順列 道順 No Youtube



重複順列 Itパスポート出題テーマ別過去問題 平成24年度秋期 テクノロジ系 問78




3講 順列 1章 場合の数と確率 問題集 高校数学a



数学i Aチェック リピート 第7章 2順列 組合せ 1 重複順列 順列 Pukiwiki



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




Spi非言語問題 重複順列 重複組み合わせ 円順列 の問題 就活の答え



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




重複組み合わせの問題を解くたった1つの方法とは 公式hは使用注意



3




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
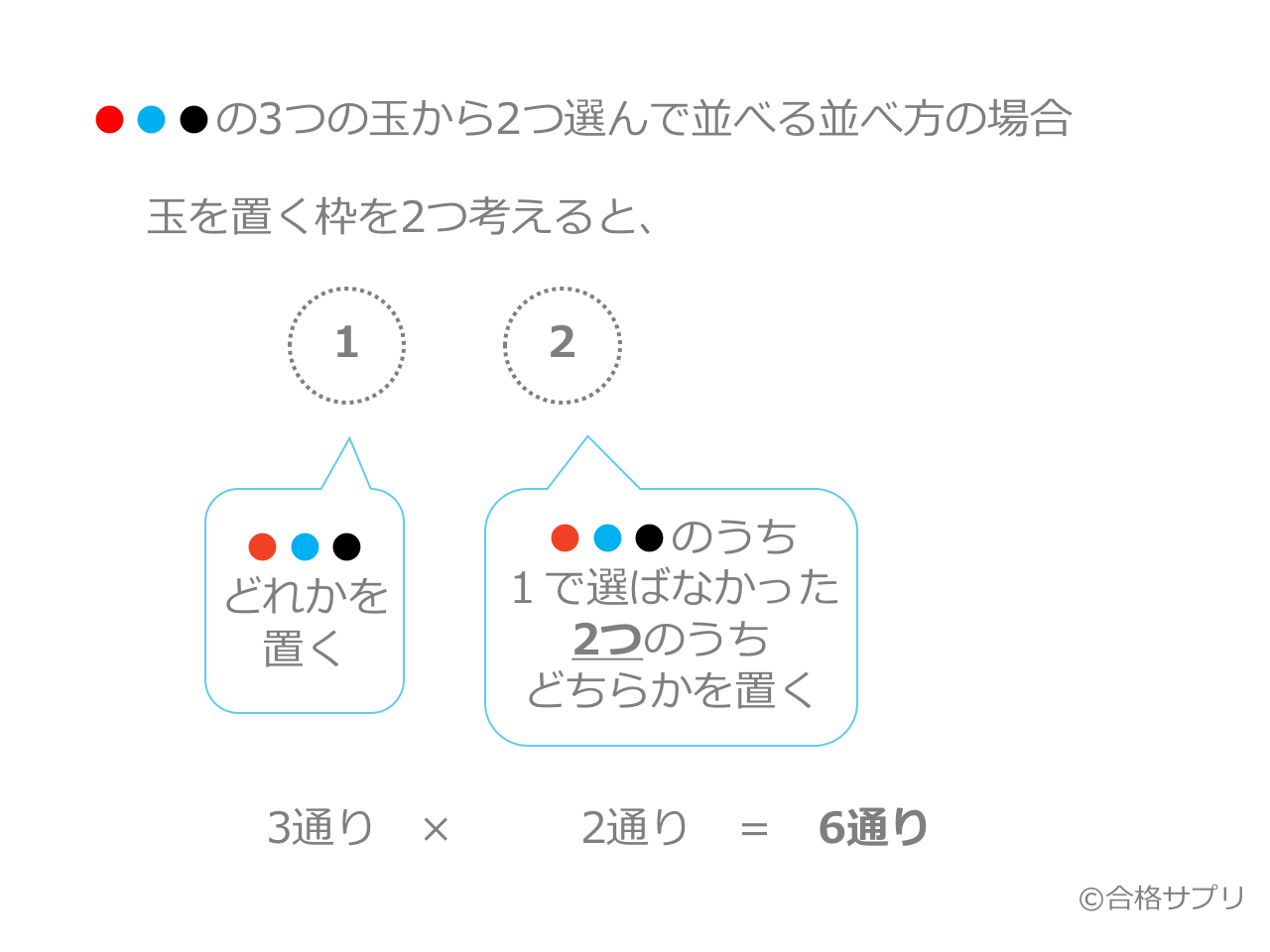



3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




高校数学 数a 7 順列 基本編 Youtube




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせの公式とその違い 問題付き 理系ラボ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長
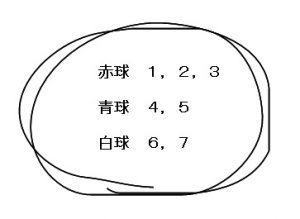



場合の数 順列と組み合わせの違いと並べ方問題の解き方



0 件のコメント:
コメントを投稿